Options Greeks: everything you need to know

What are options Greeks?

Four of these five Greeks in options trading are values which quantify the impact of certain factors on an option's price, while gamma refers to the impact on the delta:

• Δ- Delta: measures the sensitivity of the option’s price to changes in the option’s underlying asset price
• γ- Gamma: is rate of change of delta, measuring the change in delta in response to changes in the underlying asset price
• Θ- Theta: measures the sensitivity of the option’s price to the passage of time, as options tends to lose value when they get closer to their expiry date
• V- Vega: measures the sensitivity of the option’s price to changes in implied volatility
• p- Rho: measures the sensitivity of the options value to changes in the interest rate

Once you know how to use options Greeks, they could help you make better trading decisions by giving you key information.

We explain how they can be calculated below, and many of these values are usually automatically shown on our trading platform. Please note: the Greeks displayed on our platform are indicative only and are not intended to form the basis of your trading or investment decisions.

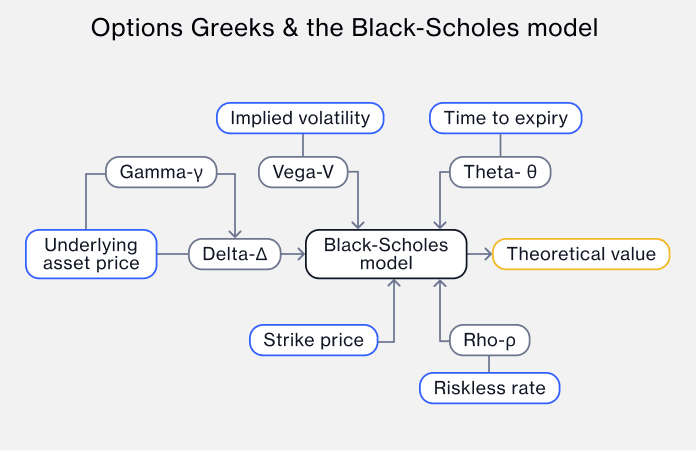
This chart displays how the five options Greeks can have an impact on various factors in involved in trading, and how they closely link to the Black-Scholes model, which is the most common way to calculate the price a trader will pay for an option.

Delta explained

Delta is the most used options Greek and estimates how much an option premium (price) will move based on a 1 unit change in the price of the option’s underlying asset. Some traders use it to indicate the probability that an options contract will expire in-the-money. It's important to note that this is an approximation and not a precise probability measure.

How does delta work?

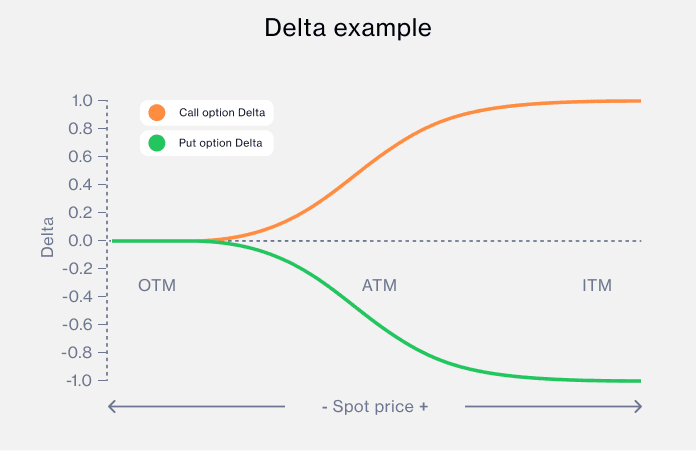
Delta is a measure of how the price of an option reacts to price changes in the underlying asset. Call options have a positive delta between 0 and 1, while put options have a negative delta between 0 and -1. For instance, a delta of 0.5 indicates the call option price would increase by £0.50 if the underlying asset’s price increases by £1.

So, a delta of 0.5 can suggest there's a roughly 50% chance the option will end up in-the-money, as the closer delta is to the 1, the higher the probability the option expires in-the-money. The rationale behind the increasing delta for in-the-money call options is based on the increasing likelihood that the option will retain its intrinsic value (the value by which the option is in-the-money). As the underlying stock price moves further above the strike price, the option gains intrinsic value, and it becomes more likely that the option will not only have intrinsic value at expiration, but also a higher sensitivity to the stock's price movement.

The delta value of an at-the-money call is typically in the middle at around 0.5, and the deeper the call is in-the-money, the nearer the delta is to 1.

The range for put options is an exact mirror: -1 to 0. The deeper an option is in-the-money, the closer it is to -1. An option with a delta value of -1 will decrease in value by £1 for every £1 increase in the underlying asset price.

How is delta calculated?

Delta = Change in an option’s price / Change in the underlying asset’s price.

For example, if a call option's price increases by £0.25 and the underlying asset price increases by £1, the call option has a delta of 0.25.

Delta = £0.25 / £1.00 = 25

Delta example

The delta of an at-the-money call option on the FTSE 100 index is 0.50. This implies that for every 1-point increase in the FTSE 100 index, the call option's price will rise by £0.50 (if no other variables change). If the FTSE 100 is trading at 7,000 points and the call option’s contract is for one index point, then the call option will give the holder control over £7,000 worth of the FTSE 100 index.

An increase in the index to 7,001 points means the call option value will go up by half a point. However, as the index climbs and the call option becomes deeper in-the-money, its delta will also increase incrementally, particularly as the contract nears expiration.

For a put option on the FTSE 100 index, with a delta of -0.50, a 1-point rise in the index will result in a £0.5 point decrease in the option's price. If the FTSE 100 increases by 1 point from 7,000 to 7,001, the price of the put option contract will decrease by £0.5.

Should the FTSE 100 index decrease to 6,999 points, the price of the put option contract would increase by £0.5. Just as with call options, the delta of a put option will adjust as the option moves further in-the-money or out-of-the-money.

As the put option moves further in-the-money, its delta approaches -1, reflecting an increased likelihood of finishing in-the-money at expiry. Conversely, as the put option moves further out-of-the-money, its delta moves closer to 0, indicating a decreased likelihood of finishing in-the-money.

Gamma explained

Gamma measures the rate of change of delta for a 1-point change in the price of the underlying asset. An option with a higher gamma indicates more risk, as the option is more likely to experience volatile swings.

How is gamma calculated?

Gamma is computed by taking the delta and the underlying asset price from two points on a timeline in the option, using the following equation:

(Delta 1 - Delta 2) divided by (Price 1 - Price 2).

Gamma example

Company X trades at $20 per share, and a $20 call option has a delta of 0.5. The price rises to $22 per share and the $20 call option's delta rises to 0.7. Therefore:

Gamma = (0.5 - 0.7) / ($20 - $22) = (-0.2) / (-2) = 0.1

If Company X shares rise by $1, the gamma (0.10) is added to the existing delta (0.50), resulting in a new delta of 0.60. If the stock's price decreased by $1, the gamma would be subtracted from the delta, giving a new delta of 0.4.

As an option moves deeper into-the-money, the delta climbs closer to 1.0. Gamma peaks when an option is at-the-money and decreases as an option moves deeper in or out-of-the-money.

How to use gamma?

Gamma helps you gauge how quickly an option’s delta will move. A higher gamma indicates an option position has greater risk and can be susceptible to larger swings in value.

Theta explained

Theta measures 'time decay', or the rate of decline in the value of an option as it gets closer to expiry. It indicates how much an option price would decrease every day assuming all other factors that determine the option remain the same. As the option expiry approaches, there's less time for the option price to make significant moves, reducing the probability of the option being 'in-the-money' (profitable) at expiry.

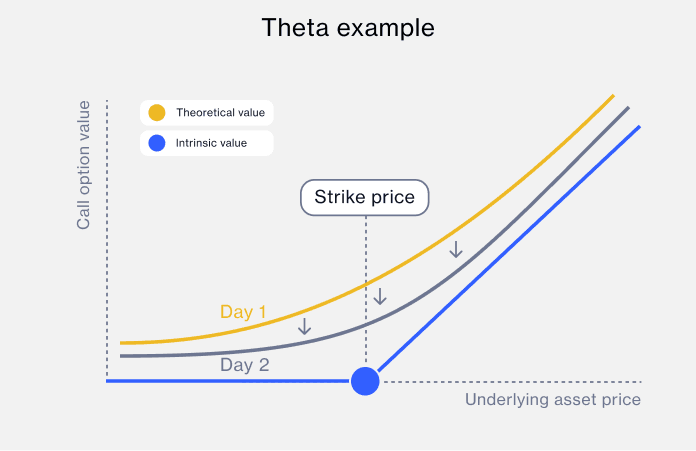
How is theta calculated?

To calculate the total theta exposure for a portfolio of options contracts, you would multiply the theta value of one option by the total number of contracts held.

Total theta exposure = number of contracts × theta per contract

If you hold 10 FTSE 100 option contracts and the theta of one option contract is currently at –0.3, your total theta exposure is -£3 per day (10 contracts × -0.3 theta per contract).

This means that, everything else remaining constant, your options position loses £3 every day.

How do you use theta?

Traders use theta and the other Greeks to compare and select options and determine the optimum timeframe.

Understanding the impact of theta on an option's value as it nears expiry can help a trader to monitor and manage their options positions more effectively.

Vega explained

Vega shows how much the option price will change given a 1 percentage point change in implied volatility. Generally, if implied volatility increases, the option price does so too, because of the higher uncertainty or risk associated with the underlying asset.

How is vega calculated?

If the implied volatility of the FTSE 100 increases by 1 percentage point, the total increase in the value of your options position would be calculated by using the following equation:

Total vega exposure = number of contracts × vega per contract

For example, if one option contract has a vega of £0.2, this means that the price of the option is expected to move £0.2 for a 1 percentage point change in implied volatility of the underlying asset.

If the vega is high, the option price is highly sensitive to the volatility of the underlying asset.

So, if you hold 10 × FTSE 100 option contracts and the vega of one option contract is £0.2, then for a 1 percentage point increase in the implied volatility of the underlying asset, the total value of your options position is expected to increase by £2 (10 contracts × £0.2 vega per contract x 1 percentage point increase).

Conversely, for a 1 percentage point decrease in implied volatility, the total value would decrease by £2.

Rho explained

Rho is seen by most traders as having the least impact of all the option Greeks. Rho measures the sensitivity of an option price to changes in interest rates. It shows how much the option price would change given a 1 percentage point change in interest rates.

Advantages of using the Greeks when trading

Options Greeks can help traders understand how various factors impact options prices. The Options Greeks displayed on our platform are indicative only and shouldn’t form the basis of your trading or investment decisions.